-
Hash Table ( 해쉬 테이블 )Computer Science/Data Structure and Algorithm 2020. 4. 1. 13:31
✔️ 테이블 자료구조
◾ 저장되는 데이터는 키(key)와 값(value)이 하나의 쌍을 이룬다.
◾ 키(key)가 존재하지 않는 값은 저장할 수 없다.
◾ 모든 키(key)는 중복되지 않는다.
◾ 테이블 자료구조는 사전구조 혹은 맵(map)이라 불리기도 한다.
✔️ 해쉬 함수와 충돌💥
◾ 해쉬 함수는 넓은 범위의 키를 좁은 범위의 키로 변경하는 역할을 한다.

해쉬 함수 ◾ 위 그림의 f(x)는 mod 100 연산을 하는 함수이다. 위 해쉬 함수를 사용하여 8자리의 키를 2자리의 키로 바꾸었다.
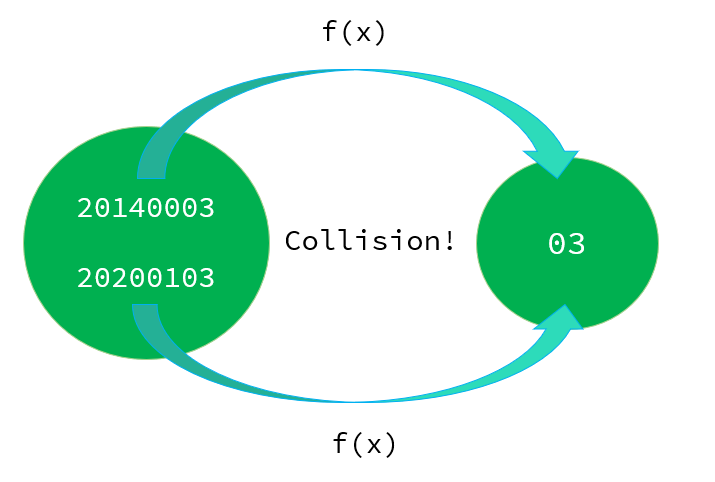
해쉬 충돌 ◾ 위 그림에서 보이듯이 서로 다른 두 개의 키가 해쉬 함수를 통과했는데, 그 결과가 03으로 동일하다. 이러한 상황을 가리켜 충돌(Collision)이라고 한다.
✔️ 좋은 해쉬 함수의 조건
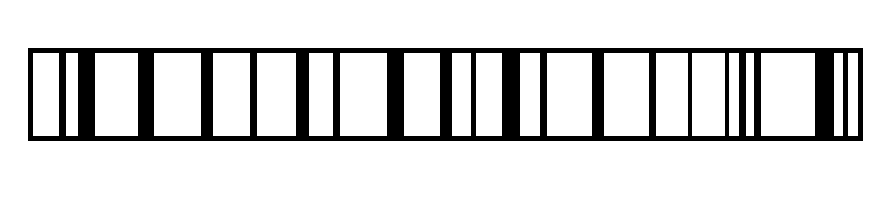
좋은 해쉬 함수를 사용한 결과 ◾ 위 그림은 테이블의 메모리 상황을 표현한 것이다. 그림에서 검은 영역은 데이터가 채워진 슬롯을 의미하고, 반대로 흰 영역은 빈 슬롯을 의미한다.
◾ 위 그림을 보면 데이터가 테이블의 전체 영역에 고루 분포 되어있다. 이는 '충돌' 발생 확률이 낮다는 것을 의미한다.
◾ 좋은 해쉬 함수는 "충돌을 덜 일으키는 해쉬 함수"라고 말할 수 있다.

좋지 않는 해쉬 함수를 사용한 결과 ◾ 위 그림에서는 테이블의 특정 영역에 데이터가 몰린 상황을 보이고 있다. 충돌이 발생할 확률이 높은 상황이다.
◾ 좋은 해쉬 함수는 키의 일부분을 참조하여 해쉬 값을 만들지 않고, 키 전체를 참조하여 해쉬 값을 만들어 낸다.
◾ 많은 수의 데이터를 조합하여(키 전부를 조합하여) 해쉬 값을 생성했을 때, 보다 다양한 값의 생성을 기대할 수 있다.
◾ 해쉬 함수 디자인 방법은 비트 추출 방법, 자릿수 폴딩 방법 등이 있다.
✔️충돌(collision) 문제의 해결책
1️⃣ 선형 조사법(Linear Probing)
◾ 충돌이 발생했을 떄, 그 옆자리가 비었는지 살펴보고, 비었을 경우 그 자리에 대신 저장하는 것이 '선형 조사법'이다.
◾ 선형 조사법의 빈자리 찾는 순서는 아래와 같이 전개 된다.
◾ f(k)+1 -> f(k)+2 -> f(k)+3 -> f(k)+4 ....
◾ 근데 이러한 선형 조사법은 충돌 횟수가 증가함에 따라 '클러스터(cluster) 현상', 쉬운 표현으로 "특정 영역에 데이터가 집중적으로 몰리는 현상'이 발생한다는 단점이 있다.
◾ "좀 더 멀리서 빈공간을 찾으면 되지 않을까?" 라는 생각을 근거로 탄생한 것이 '2차 조사법'이다. 충돌 발생시 2차 조사법의 빈자리 찾는 순서는 아래와 같이 전개 된다.
◾ f(k)+1^2 -> f(k)+2^2 -> f(k)+3^2 -> f(k)+4^2 ....
◾ 선형 조사법은 충돌 발생시 n칸 옆의 슬롯을 검사한다면, 이차 조사법은 N^2칸 옆의 슬롯을 검사한다.
2️⃣ 이중 해쉬
◾ 2차 선형 조사법의 문제점은 다음과 같다. "해쉬 값이 같으면, 충돌 발생시 빈 슬롯을 찾기 위해서 접근하는 위치가 늘 동일하다." 선형 조사법보다는 낫지만, 접근이 진행되는 슬롯을 중심으로 클러스터 현상이 발생할 확률은 여전히 높다.
◾ "2차 조사법은 빈 공간을 찾는 방식이 1칸, 2칸, 9칸, 16칸.. 이렇게 규칙적이다. 이것을 불규칙하게 구성하면 어떨까?" 이런 생각에서 출발한 것이 '이중 해쉬'이다.
◾ 이중 해쉬는 아래와 같이 두 개의 해쉬 함수를 사용한다.
◾ 1차 해쉬 함수 : 키를 근거로 저장위치를 결정하기 위한 것
◾ 2차 해쉬 함수 : 충돌 발생시 몇 칸 뒤를 살필지 결정하기 위한 것
🔍이중 해쉬 예제
🔹 1차 해쉬 함수 : H1(k) = k % 15
🔹 2차 해쉬 함수 : H2(k) = 1+ ( k % c )
위의 2차 해쉬 함수는 일반적인 형태이다. 1차 해쉬 함수를 %15로 결정한 것으로 보아, 배열의 길이가 15라고 예상해 볼 수 있다. 이런 경우 2차 해쉬 함수의 상수 c는 15보다 작은 소수 중 하나로 결정하게 된다. 따라서 다음과 같이 1,2차 해쉬 함수를 결정할 수 있다.
🔹 1차 해쉬 함수 : H1(k) = k % 15
🔹 2차 해쉬 함수 : H2(k) = 1+ ( k % 7 )
2차 해쉬 함수는 왜 위와 같은 형태일까? 먼저 1을 더하는 이유는 2차 해쉬 값이 0이 되는 것을 막기 위해서이다. 충돌 발생 이후 다른 자리를 살피는 상황에서 2차 해쉬값은 0이 되면 안된다. 15보다 작은 값으로 결정하는 이유는 2차 해쉬 값이 1차 해쉬 값을 넘어서지 않게 하기 위함이고, 소수로 결정하는 이유는 소수를 선택했을 때 클러스터 현상의 발생 확률을 현저히 낮춘다는 통계가 있기 때문이다.
정의한 1,2차 해쉬 함수에 키가 18, 33인 데이터를 순서대로 저장하면 충돌이 발생한다.
🔹 H1(18) = 18 % 15 = 3
🔹 H1(33) = 33 % 15 = 3
🔹 H2(18) = 1 + 18 % 7 = 5
🔹 H2(33) = 1+ 33 % 7 = 6
위에서 보이듯 1차 해쉬 값이 같아도 2차 해쉬 값은 다르다. 그리고 이 2차 해쉬 값을 근거로 빈 슬롯을 찾는 과정은 각각 다음과 같이 전개된다.
🔹 H1(18) -> H1(18) + 5 x 1 -> H1(18) + 5 x 2 -> H1(18) + 5 x 3 ....
🔹 H2(33) -> H1(33) + 6 x 1 -> H1(33) + 6 x 2 -> H1(33) + 6 x 3 ....
위와 같이 1차 해쉬 값을 기준으로 2차 해쉬 값의 크기만큼 건너 뛰면서 빈 슬롯을 찾게 되므로, 키가 다르면 건너 뛰는 길이도 달라진다. 따라서 클러스터(cluster) 현상의 발생 확률을 현저히 낮출 수 있다. 참고로 실제로 이중 해쉬는 이상적인 충돌 해결책으로 알려져있다.
3️⃣ 체이닝(Chaining) ⛓️
◾ 선형조사법과 이중 해쉬는 충돌이 발생하면 다른자리에 대신 저장하는 방법이다. 이를 '열린 어드레싱 방법(open addresing method)'이라고 한다.
반면, 체이닝은 무슨 일이 있어도 자신의 자리에 데이터를 저장한다. 이를 '닫힌 어드레싱 방법(closed addresing method)'이라 한다.
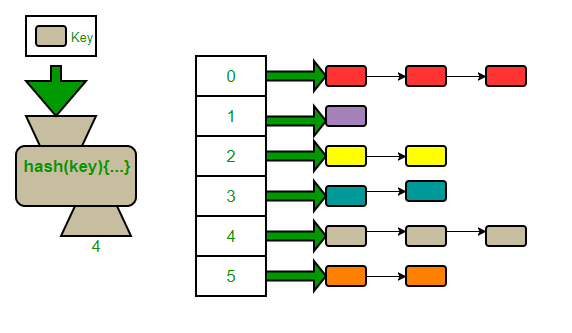
chaining ◾ 위 그림 처럼 슬롯을 생성하여 연결리스트의 모델로 연결해나가는 방식으로 충돌 문제를 해결하는 것이 '체이닝' 방법이다.
◾ 그림을 보면 알 수 있겠지만, 체이닝을 하면 하나의 해쉬 값에 다수의 슬롯을 둘 수 있다.
◾ 탐색을 위해서 동일한 해쉬 값으로 묶여있는 연결된 슬롯들을 모두 조사해야 한다는 불편이 있지만, 해쉬 함수를 잘 정의한다면, 그래서 충돌의 확률이 높지않다면 연결된 슬롯의 길이는 부담스러운 정도가 아닐 것이다.
윤성우 자료구조 책 참고
'Computer Science > Data Structure and Algorithm' 카테고리의 다른 글
Tree, Binary Search Tree, AVL Tree (0) 2020.04.02 Stack, Queue, Deque ( 스택, 큐, 덱 ) (0) 2020.04.02 Array, Linked List ( 배열, 연결리스트 ) (0) 2020.04.02 Big-O (시간 복잡도, 공간 복잡도) (0) 2020.04.02 Divide and Conquer ( 분할 정복 ) (0) 2020.04.02