Big-O (시간 복잡도, 공간 복잡도)

✔️ 개요

◾ 우리는 잘 동작하는 알고리즘은 물론이거니와 좋은 성능의 알고리즘을 설계 해야한다. 따라서 우리는 자료구조와 알고리즘을 분석하고 평가할 수 있어야 한다.

◾ 알고리즘을 평가하는 요소는 두 가지 요소는 '속도'와 '메모리 사용량'이다.

◾ '속도'에 해당하는 알고리즘의 수행시간 분석결과를 가리켜 '시간 복잡도(time complexity)라고 한다. 

◾ '메모리 사용량'에 대한 분석결과를 가리켜 '공간 복잡도(space complexity)'라고 한다. 

◾ 일반적으로는 알고리즘을 평가할 때 메모리 사용량보다 실행속도에 초점을 둔다.

◾ 우리는 '속도'를 측정하기 위해 알고리즘의 연산 횟수를 센다. 그리고 처리해야할 데이터의 수 n에 대한 연산횟수의 함수를 구성한다. 

◾ Big-O는 '데이터 수의 증가'에 따른 '연산횟수의 증가 형태를 표현한 것'이다.

---

✔️ 시간복잡도 ( Time Complexity )

◾ Big-O 시간은 알고리즘의 효율성을 나타내는 지표이다.

◾ 예를들어 너비가 w미터이고 높이가 h미터인 울타리를 색칠하는 데 소요되는 시간은 O(wh)로 표기할 수 있다. 만약 페인트를 p번 덧칠해야한다면, O(pwh)의 시간이 소요된다고 말할 수 있다. 

◾ 가장 흔하게 사용되는 Big-O 시간은 다음과 같다. O(logN), O(NlogN), O(N), O(N^2), O(2^N)

◾ 알고리즘의 수행시간은 최선의 경우, 최악의 경우, 평균적인 경우 3가지로 나누어 볼 수 있다.

◾ 최선의 경우는 쓸만한 개념이 아니다. 최선의 경우는 결국 아무 알고리즘이나 취한 뒤 특수한 입력을 넣으면, O(1)시간에 동작하도록 만들 수 있다.

◾ 대부분의 알고리즘은 최악의 경우와 평균적인 경우가 같다. 가끔 이들이 달라서, 최악과 평균 두 경우 모두 언급해야 되기도 한다. 

◾ Big-O에서는 상수항과 지배적이지 않은 항은 무시한다. ( 가장 큰 차수의 항이 전체 수식에 주는 영향이 매우 크기 때문이다. ) 예를들어 O(2N^2 + 3n +4) 시간은  O(N^2) 이라고 표기한다. 

 

---

✔️ 공간복잡도 ( Space Complexity )

◾ 알고리즘에서는 시간뿐 아니라 메모리 또한 신경 써야 한다.

◾ 크기가 N인 배열을 만들고자 한다면, O(N)의 공간이 필요하다.

◾ NxN 크기의 2차원 배열을 만들고자 한다면, O(N^2)의 공간이 필요하다.

 

---

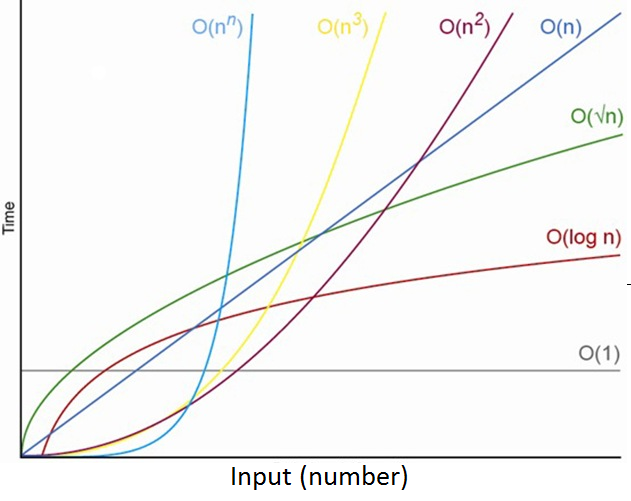
👀 시각화