Tree, Binary Search Tree, AVL Tree

✔️ Tree(트리)

◾ 트리는 계층적 관계를 표현하는 자료구조이다.

◾ 트리는 부모 노드와 자식 노드의 관계로 재귀적으로 구성된다. 부모 노드가 없는 노드를 루트노드라고 정의한다.

◾ 노드(node) : 트리의 구성요소

◾ 간선(edge) : 노드와 노드를 연결하는 연결선

◾ 루트 노드(root node) : 트리 구조에서 최상위에 존재하는 노드

◾ 내부 노드(internal node) : 단말 노드를 제외한 모든 노드

◾ 단말 노드(leaf node) : 아래로 또 다른 노드가 연결되어 있지 않는 노드

◾ 노드 간에는 부모, 자식, 형제 관계가 성립된다.

 

 

 

tree

 

 

 

---

✔️ Binary Tree(이진 트리)

◾ 이진트리는 각 노드가 최대 두 개의 자식 노드를 갖는 트리이다.

◾ 전위 순회(Pre oder traversal) : “현재 노드 -> 왼쪽 가지 -> 오른쪽 가지” 순으로 조회

◾ 중위 순회(Inorder traversal) : “왼쪽 가지 -> 현재 노드 -> 오른쪽 가지” 순으로 조회

◾ 후위 순회(post order traversal) : “왼쪽 가지 -> 오른쪽 가지 -> 현재 노드” 순으로 조회

 

👀 시각화

 

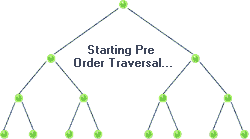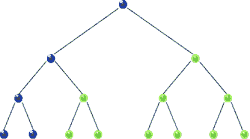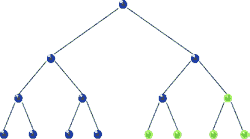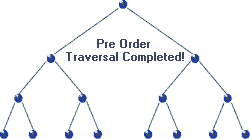
전위 순회(Pre oder traversal)

 

 

중위 순회(Inorder traversal)

 

 

후위 순회(post order traversal)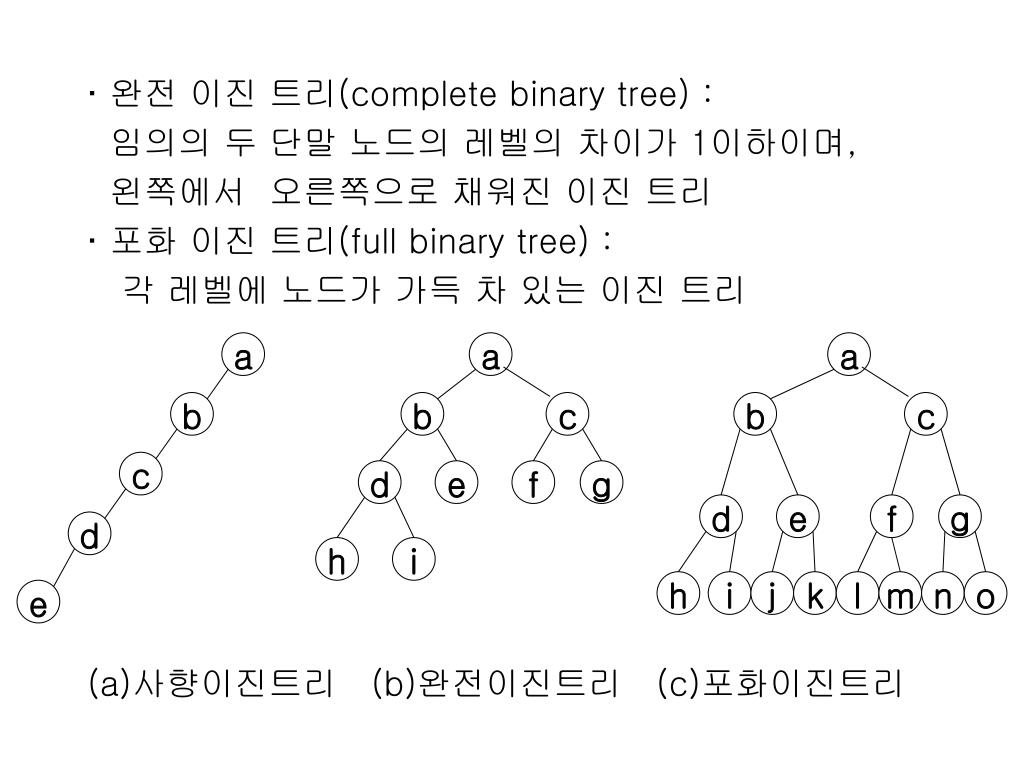

 

이진 트리의 종류

 

---

✔️ BST(Binary Search Tree, 이진 탐색 트리)

◾ 이진 탐색 트리의 노드에 저장된 키(key)는 유일하다.

◾ 루트 노드의 키가 왼쪽 서브 트리를 구성하는 어떠한 노드의 키 보다 크다.

◾ 루트 노드의 키가 오른쪽 서브 트리를 구성하는 어떠한 노드의 키 보다 작다.

◾ 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.

◾ 왼쪽 자식 노드의 키 < 부모 노드의 키 < 오른쪽 자식 노드의 키

 

⏱️ 시간 복잡도

◾ 탐색(BST가 완전 이진트리에 가깝게 구성 될 때) : BST의 탐색 연산은 O(log2N)의 시간 복잡도를 가진다. (트리의 높이가 하나씩 증가할수록 추가할 수 있는 노드 수가 두 배씩 증가하기 때문)

◾ 탐색(BST가 한쪽으로 기울어진 사향트리가 될 때) : BST의 탐색 연산은 O(N)에 가까운 시간 복잡도를 가진다. 

 

👀 시각화

 

 

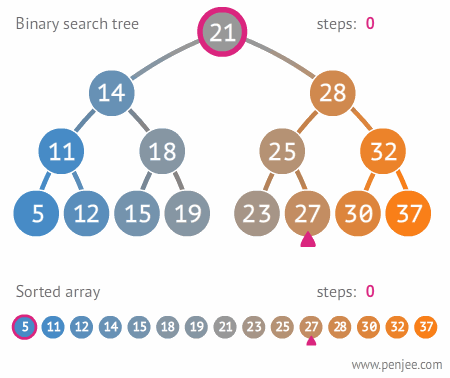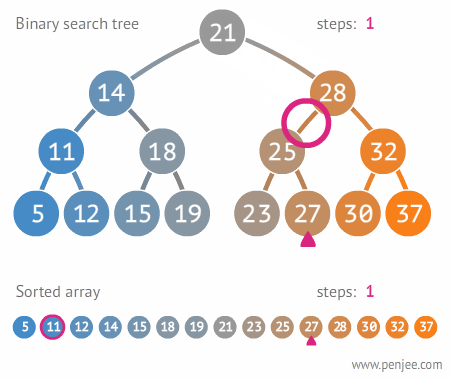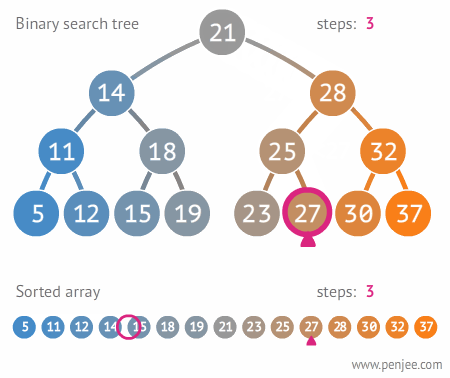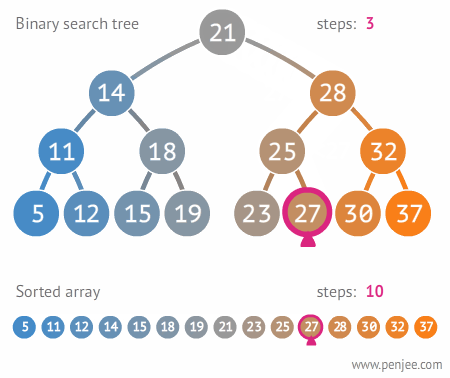
BST

 

 

BST insert

 

균형이 맞지 않으면, O(n)에 가까운 시간 복잡도를 보인다.

 

---

✔️AVL 트리

 

AVL 트리 애니매이션