-
Minimum Spanning Tree (Kruskal, Prim)Computer Science/Data Structure and Algorithm 2020. 4. 26. 22:04
✔️ Spanning Tree
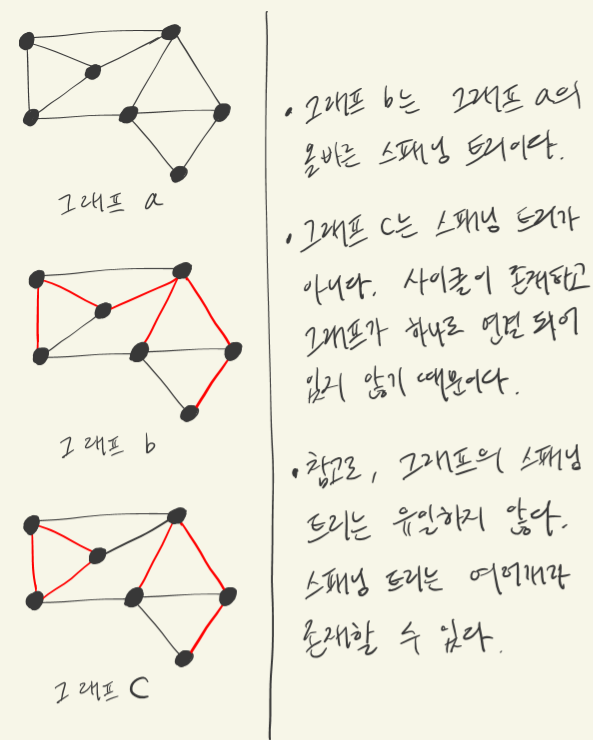
◾️ 스패닝 트리는 원본 그래프의 정점 전부와 간선의 부분 집합으로 이루어진 부분 그래프이다.
◾️ 스패닝 트리에 포함된 간선들은 정점들을 트리 형태로 전부 연결해야한다.
◾️ 트리 형태란 간선들이 사이클을 이루지 않는다는 것을 의미한다.
✔️ Minimum Spanning Tree Problem
◾️ 최소 스패닝 트리 문제란, 가중치 그래프의 스패닝 트리 중 가중치의 합이 가장 작은 트리를 찾는 문제를 말한다.
◾️ 즉, 그래프의 연결성을 그대로 유지하는 가장 '저렴한' 그래프를 찾는 문제이다.
✔️ Kruskal's Algorithm
◾️ 크루스칼의 최소 스패닝 트리 알고리즘은 그래프의 모든 간선을 가중치의 오름차순으로 정렬한 뒤, 스패닝 트리에 하나씩 추가해 나간다. 이때, 사이클을 형성할 수 있는 간선은 추가하지 않는다.
◾️ 아래는 자세한 구현 설명이다.
- 간선의 목록을 얻어서 오름차순으로 가중치를 정렬한다.
- 간선 목록을 순회하면서, 이들을 스패닝 트리에 추가한다.
- 스패닝 트리에 간선을 추가할 때, 해당 간선이 사이클을 만드는지 확인 해야한다. 이는 간선의 두 정점이 같은 집합에 존재하는지 확인하면 된다. 이 때, Union Find 자료구조를 사용한다.
- 사이클 여부를 판단하기 위해 Find 연산을 활용하고, 사이클을 만들지 않을 경우에는 Union 연산으로 두 집합을 합친다. (Union-Find 참고 : https://kpuls.tistory.com/62?category=845292)

👨💻 Kruskal's Algorithm의 구현
◾️ 크루스칼 알고리즘을 설명할때 Union-Find 자료구조를 사용한다고 설명했다. 코드상의 DistjointSet은 Union-Find 자료구조이다.
#include<vector> #include<algorithm> using namespace std; struct DisjointSet; const int MAX_V = 100; int V; //정점의 개수 vector<pair<int, int>> adj[MAX_V]; //그래프의 인접리스트. (연결된 정점 번호, 간선 가중치) 쌍을 담는다. //주어진 그래프에 대해 최소 스패닝 트리에 포함된 간선의 목록을 selected에 저장하고, //가중치의 합을 반환한다. int kruskal(vector<int, pair<int, int>>& selected) { int ret = 0; selected.clear(); // (가중치, (정점1, 정점2)) 목록을 얻는다. vector <pair<int, pair<int, int>>> edges; for (int u = 0; u < V; u++) { for (int i = 0; i < adj[u].size(); i++) { int v = adj[u][i].first, cost = adj[u][i].second; edges.push_back({ cost, {u,v} }); } } //간선을 가중치 순으로 정렬한다. sort(edges.begin(), edges.end()); //처음엔 모든 정점이 분리되어있다. DisjointSet sets(V); //간선 목록을 조회하면서, 스패닝 트리를 만들어나간다. for (int i = 0; i < edges.size(); i++) { int cost = edges[i].first; int u = edges[i].second.first, v = edges[i].second.second; //u와 v가 같은 집합이라면, u-v 간선을 추가했을때 사이클을 형성하므로 //간선을 추가하지 않는다. if (sets.find(u) == sets.find(v)) continue; //u-v간선을 추가한다.(u, v가 속한 두 집합을 합친다.) set.doUnion(u, v); //간선 목록에 간선 추가 selected.push_back({ u,v }); //가중치 추가 ret += cost; } return ret; }✔️ Prim's Algorithm(추가 예정)
'Computer Science > Data Structure and Algorithm' 카테고리의 다른 글
Shortest Path Algorithm (0) 2020.05.20 Sieve of Eratosthenes (0) 2020.04.28 Union Find, Disjoint Set (0) 2020.04.24 Brute Force - Bit Masking (0) 2020.04.20 Graph (0) 2020.04.02